L'exercice 9 et son corrigé se trouve à ce lien à 1h 19min et 11 secondes Relativité restreinte (2020-2021), exercices 2 (youtube.com). J'ai voulu continuer cette exercice via l'analyse numérique.
Ci-dessous, voici l'énoncé.
L'énoncé
Exercice 9 : Attentat interstellaire
Derrière le comptoir improbable du bar le plus mythique de la Galaxie, Quark, le fameux barman, raconte, sourire en coin, l’étrange histoire suivante à trois clients de passage. Dans la paix magistrale des espaces inter-sidéraux, l’élégant vaisseau de la princesse Amidala, exceptionnellement réduit pour plus dediscrétion à une longueur de 100 mètres, filait à travers le royaume à vitesse constante (par rapport au référentiel Galactique, supposé galiléen), correspondant à un facteur de Lorentzγ= 4.Sur le chemin du vaisseau spatial, un dispositif avait été installé par les sombres agents de la Guilde des Ténèbres, composé de deux bombes, immobiles dans le référentiel Galactique, et séparées par une distance égale elle aussi à 100 mètres, le long de la trajectoire que, selon leurs informations, le vaisseau allait emprunter. Et voici qu’à l’instant même où le milieu du vaisseau arrivait juste à la position du milieu des deux bombes... ces dernières ont explosé !
–Ouf !, soupire le premier client, les explosions n’auront fait qu’effleurer la carlingue, à la poupe comme à la proue. Heureusement que le vaisseau n’ était pas plus grand ! Mais le deuxième client est devenu pâle.
–Votre ignorance vous aveugle ! , s’exclame-t-il horrifié. Dans quel espace-temps vivez-vous ? N’avez-vous jamais entendu parler de la contraction des longueurs ? Dans son vaisseau, notre noble princesse était certes sereine, au repos dans son propre référentiel. Mais les bombes, elles, immobiles par rapport au référentiel Galactique, se déplaçaient par rapport au vaisseau à trés grande vitesse. Toutes leurs longueurs mesurées le long de l’axe du mouvement étaient donc contractées d’un facteur γ= 4. Dans le référentiel du vaisseau, la distance entre les deux bombes n’ était donc pas de 100 mètres, leur distance propre, mais de 25 mètres ! Le vaisseau a dû être pulvérisé... et la princesse avec !
–Mais c’est horrible !, s’ écrit alors le premier, se souvenant enfin de ses cours de Physique d’Ecole primaire. C’est alors qu’intervient le troisième client du bar, que Quark venait de resservir :
–Cessez de pleurnicher !, trancha-t-il. La princesse est en vie, j’en atteste ! Puisque le vaisseau se déplaçait avec un facteur de Lorentz de 4, sa longueur propre de 100 mètres n’était plus que de 25 mètres dans le référentiel Galactique. Les deux bombes ont donc fait feu bien loin de la carlingue. Soyez-en assurés : Amidala n’aura eu aucune égratignure ! Quels tocards, quand même, ces losers de la Guilde !
QUESTION : Qui a raison ?
[NB : ne jamais hésiter à décrire précisément la situation telle qu’elle se présente dans les différents référentiels, en raisonnant sur les evénements quadri-dimensionnels, comme il se doit, plutôt que séparément sur les points de l’espace et les instants.]
Réponse
Résultat
Dans le cas où les bombes explosent au même instant dans le référentiel galactique et que le facteur de Lorentz est de 2, alors le vaisseau sort indemne de l'attentat. Pour s'en convaincre, on calculera la distance des 4 événements suivants en utilisant la métrique de Minkowski dans chacun des référentiels.
Afin d'introduire quelques noms (s1, s2, b1, b2 et E), voici un schéma
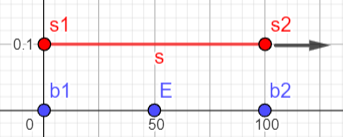
Ainsi, on calculera (Es1-Eb1) ou de (Es2-Eb2) qui correspond à la distance quadri-dimensionnel entre l'événement de l'arrière du vaisseau lorsque la première bombe explose et l'événement de la première bombe qui explose dans le référentiel galactique. Je ferai la même chose pour l'avant du vaisseau avec la seconde bombe. Et je calculerai ces 2 distances dans les 3 référentiels. Le référentiel galactique (ℜg), le référentiel du vaisseau (ℜs) ('s' pour starship) et enfin pour le référentiel intermédiaire (ℜo) ('o' pour other).
Analyse quantitative et graphique
Choix des unités des axes
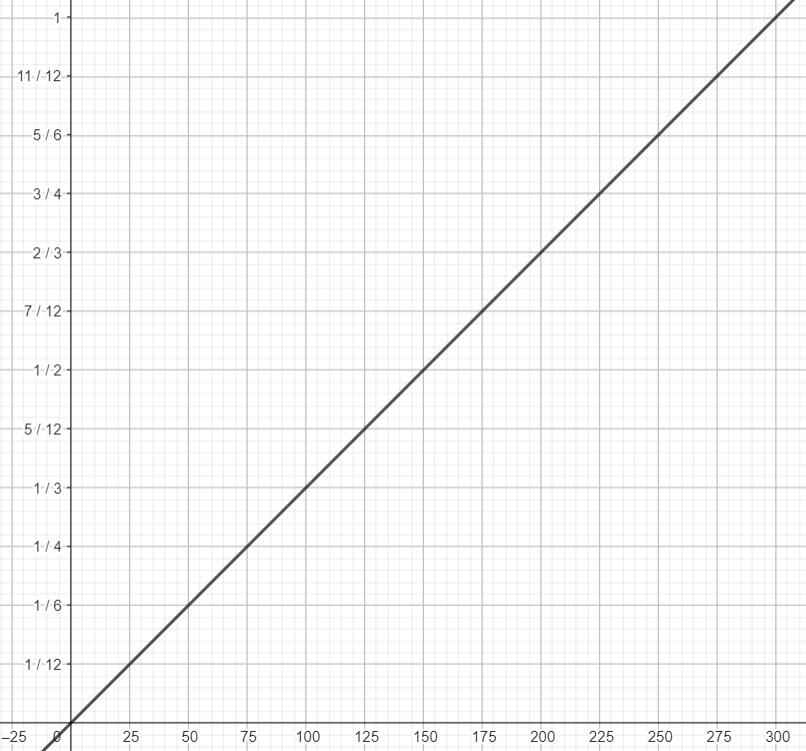
Mouvement des référentiels par rapport à ℜg
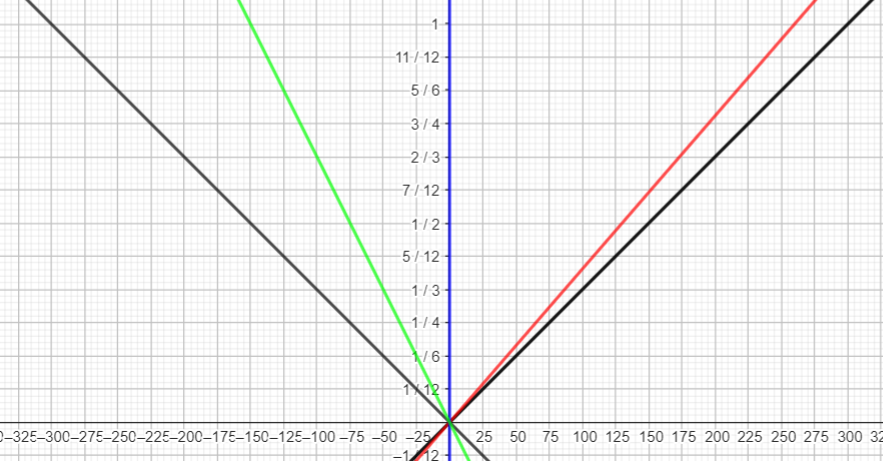
Erreur de pensée
Bien sûr, je ne peux pas déduire la vitesse de ℜo par rapport à ℜs par la logique suivante :
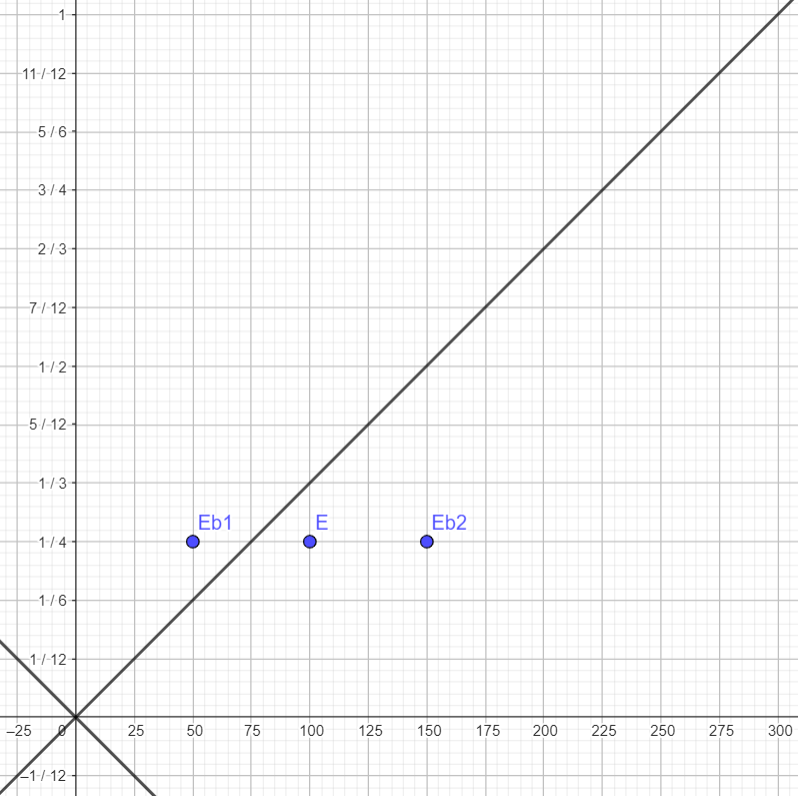
Choix arbitraire d'un repère et placement des événements dans les 3 référentiels.
Attaquons le problème maintenant par le choix de repères arbitraires pour y placer ensuite les événements.
| ℜg | ℜs | ℜo |
 |
 |
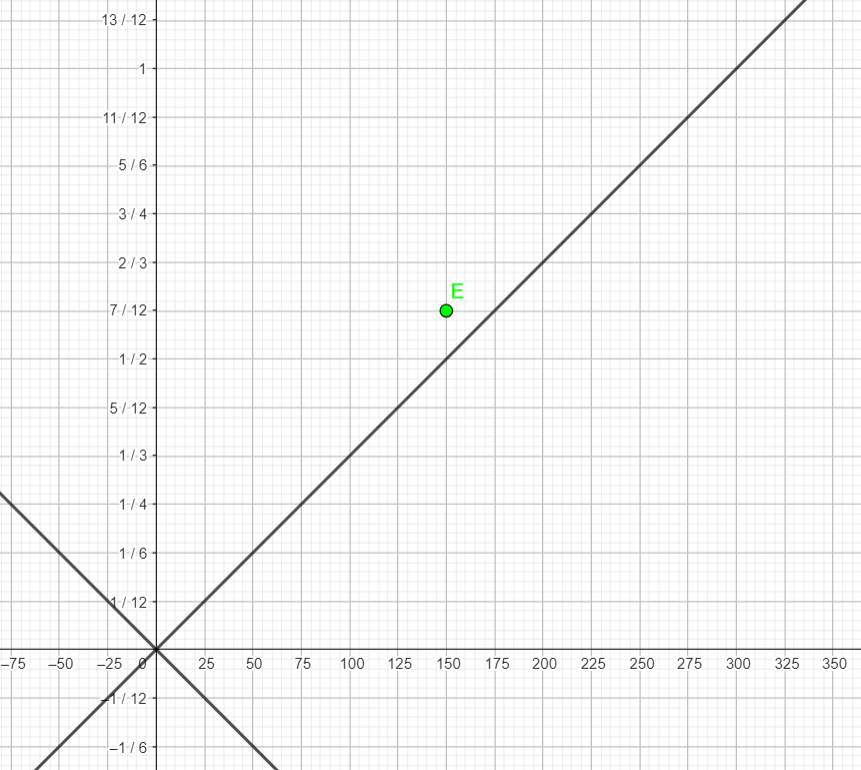 |
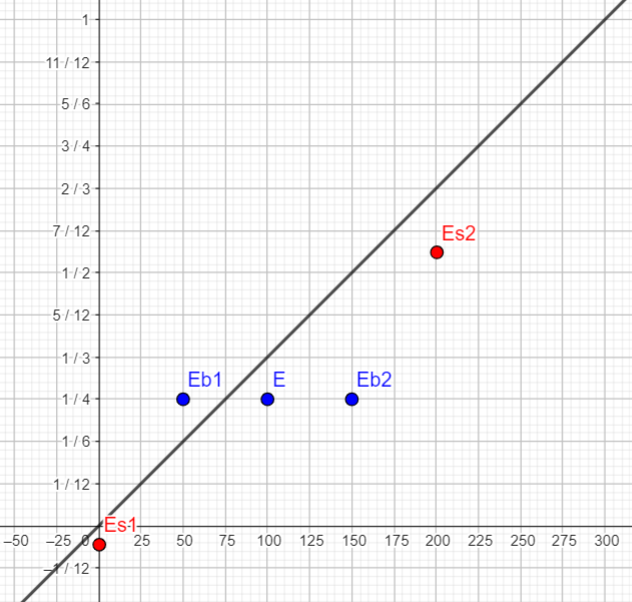
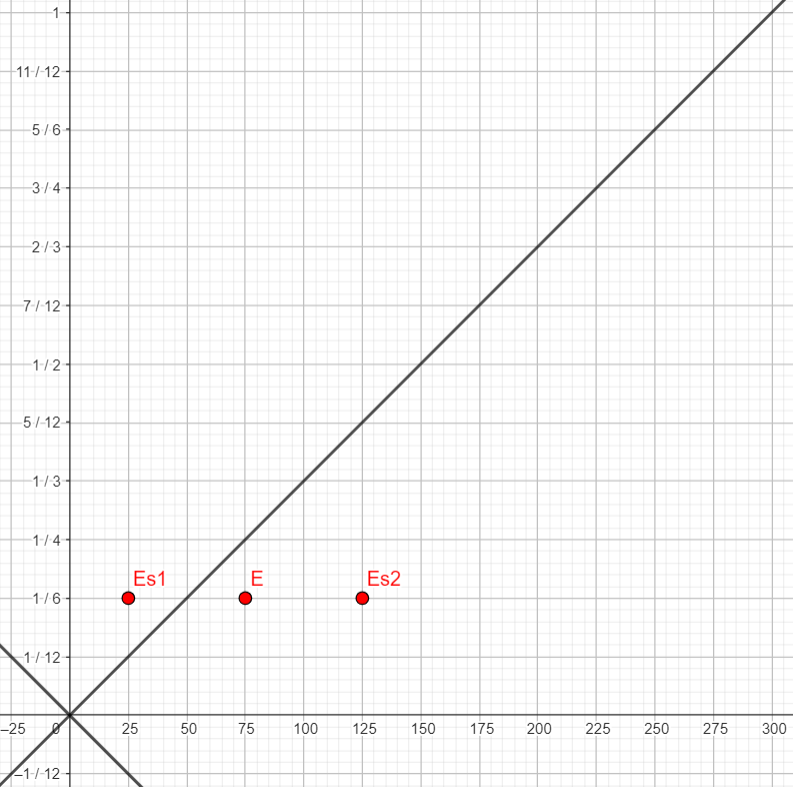
| E se produit à t = 1/4μs et x=100m (choix arbitraire) | E se produit à t = 1/6μs et x=75m (choix arbitraire) | E se produit à t = 7/12μs et x=150m (choix arbitraire) |
| Eb1 se produit à t = 1/4μs et x=50m | Eb1 sera à déterminer | Eb1 sera à déterminer |
| Eb2 se produit à t = 1/4μs et x=150m | Eb2 sera à déterminer | Eb2 sera à déterminer |
| Es1 sera à déterminer | Es1 se produit à t = 1/6μs et x=25m | Es1 sera à déterminer |
| Es2 sera à déterminer | Es2 se produit à t = 1/6μs et x=125m | Es2 sera à déterminer |
Placement des événements des autres référentiels.
C'est à ce stade, qu'apparait la transformée spéciale de Lorentz.

| ℜg | ℜs | ℜo |
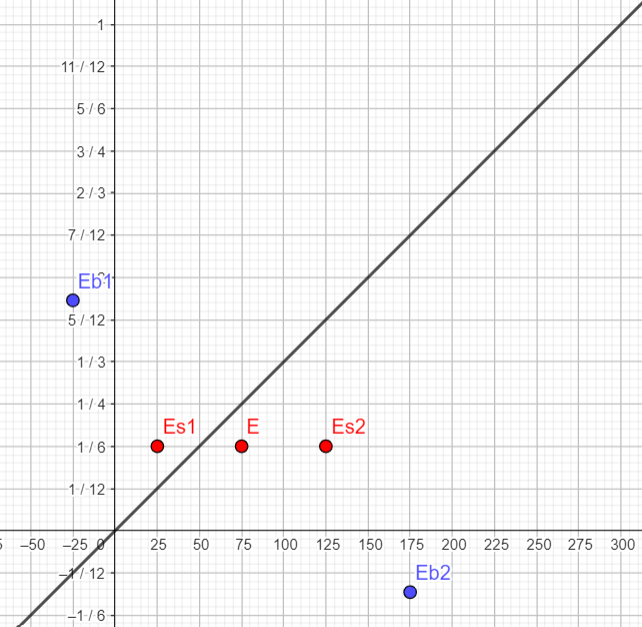
| E se produit à t = 1/4μs et x=100m | E se produit à t = 1/6μs et x=75m (choix arbitraire) | E se produit à t = 7/12μs et x=150m |
| Eb1 se produit à t = 1/4μs et x=50m | Eb1 sera à déterminer | Eb1 sera à déterminer |
| Eb2 se produit à t = 1/4μs et x=150m | Eb2 sera à déterminer | Eb2 sera à déterminer |
| Es1 sera à déterminer | Es1 se produit à t = 1/6μs et x=25m | Es1 sera à déterminer |
| Es2 sera à déterminer | Es2 se produit à t = 1/6μs et x=125m | Es2 sera à déterminer |
|
On calcule E de ℜg dans ℜs. Puis on calculera la différence entre les 2 événements ce qui donnera le décalage à appliquer aux autres événements b1 et b2 E = | t' = 2 ( 1/4*10-6 - 260*106 / (300*106)² * 100 ) = -7.6*10-8 s
| x' = 2 ( 100 - 260*106 * 1/4*10-6) = 70 m
|
On calcule E de ℜg dans ℜo. Puis on calculera la différence entre les 2 événements ce qui donnera le décalage à appliquer aux autres événements b1, b2, s1 et s2
E = | t' = 1.1547 ( 1/4*10-6 - (-150*106 / (300*106)²) * 100 ) = 4.80*10-7 s
| x' = 1.1547 ( 100 - (-260*106 * 1/4*10-6)) = 158.7 m
|
|
|
|
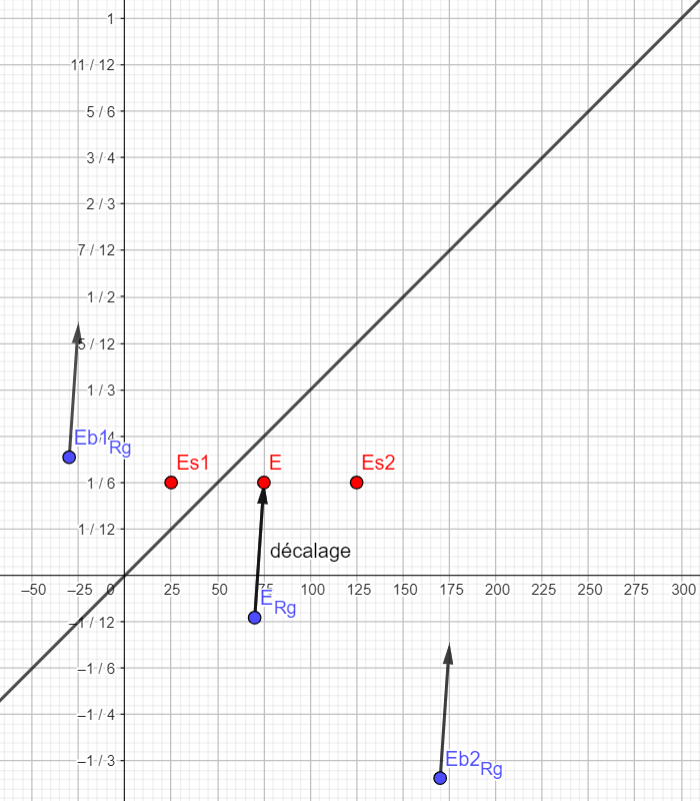
Décalage dans le repère
décalage | = t' + (1*10-6/6 - -7.6*10-8) = t' + 2.43*10-7
| = x' + (75-70) = x' + 5
|
Décalage dans le repère
décalage | = t' + (0.5*10-6 - 4.8*10-7) = t' + 0.2*10-7
| = x' + (150-158.7) = x' - 8.7
|
|
Içi je reprends le décalage dans ℜs que j'inverse
Coordonnées de Es1 | t = 1/6μs
| x=25m
Nouvelles coordonnées après décalage
Es1 | = t - 2.43 * 10-7 = 1*10-6/6 - 2.43 * 10-7 = -7.63 * 10-8 s
| = x - 5 = 125 - 5 = 20 m
Coordonnées de Es2 | t = 1/6μs
| x=125m
Nouvelles coordonnées après décalage
Es2 | = t - 2.43 * 10-7 = 1*10-6/6 - 2.43 * 10-7 = -7.63 * 10-8 s
| = x - 5 = 25 - 5 = 120 m
|
Eb1 = | t' = 2 ( 1/4*10-6 - 260*106 / (300*106)² * 50 ) = 2.12*10-7 s
| x' = 2 ( 50 - 260*106 * 1/4*10-6) = -30 m
Eb2 = | t' = 2 ( 1/4*10-6 - 260*106 / (300*106)² * 150 ) = -3.64*10-7 s
| x' = 2 ( 150 - 260*106 * 1/4*10-6) = 170 m
|
Eb1 = | t' = 1.1547 ( 1/4*10-6 - (-150*106 / (300*106)²) * 50 ) = 3.85*10-7 s
| x' = 1.1547 ( 50 - (-150*106 * 1/4*10-6)) = 101.0 m
Eb2 = | t' = 1.1547 ( 1/4*10-6 - (-150*106 / (300*106)²) * 150 ) = 5.77*10-7 s
| x' = 1.1547 ( 150 - (-150*106 * 1/4*10-6)) = 216.3 m
Es1 = | t' = 1.1547 ( -3.7*10-8 - (-150*106 / (300*106)²) * 0.32 ) = -4.20*10-8 s
| x' = 1.1547 ( 0.32 - (-150*106 * 1/4*10-6)) = -6.0 m
Es2 = | t' = 1.1547 ( 5.4*10-7 - (-150*106 / (300*106)²) * 200.3 ) = 1.00*10-6 s
| x' = 1.1547 ( 200.3 - (-150*106 * 5.4*10-6)) = 324.6 m
J'ajoute un événement E2 qui correspond à l'événement E mais quelques microsecondes plus tôt. Ceci me permettra de placer la ligne des temps sans avoir à avoir recours à la loi de composition des vitesses relativistes.
Coordonnées de E2 | t = 1/12μs
| x=75m
Nouvelles coordonnées après décalage
E2 | = t - 2.43 * 10-7 = 0.83 - 2.43 * 10-7 = -16.0 * 10-8 s
| = x - 5 = 75 - 5 = 70 m
Je calcule ces coordonnées dans Rg
E2 = | t' = 2 ( -16.0*10-8 - (-260*106 / (300*106)²) * 70 ) = 0.844*10-7 s
| x' = 2 ( 70 - (-260*106 * -16.0*10-8 ) = 56.8 m
E2 = | t' = 1.1547 ( 0.844*10-7 - (-150*106 / (300*106)²) * 56.8 ) = 2.1*10-7 s
| x' = 1.1547 ( 56.8 - (-150*106 * 0.844*10-7)) = 80.2 m
|
 |
 |
|
|
Es1 = | t' = 2 ( -7.63*10-8 - (-260*106 / (300*106)²) * 20 ) = -3.70*10-8 s
| x' = 2 ( 20 - (-260*106) * -7.63*10-8 ) = 0.32 m
Es2 = | t' = 2 ( -7.63*10-8 - (-260*106 / (300*106)²) * 120 ) = 5.40*10-7 s
| x' = 2 ( 120 - (-260*106 * -7.63*10-8 ) = 200.3 m
|
Après décalage
Eb1 = | t' = 2.12 * 10-7 + 2.43 *10-7 = 4.55 * 10-7 s
| x' = -30 + 5 = -25
Eb2 = | t' = -3.64*10-7 + 2.43 *10-7 = -1.214 * 10-7 s
| x' = 170 + 5 = 175 m
|
Rappel du décalage :
décalage | = t' + (0.5*10-6 - 4.8*10-7) = t' + 0.2*10-7
| = x' + (150-158.7) = x' - 8.7
Eb1 = | t' = 3.85*10-7 s + 0.2*10-7 = 4.05*10-7 s
| x' = 101.0 m - 8.7 = 92.3 m
Eb2 = | t' = 5.77*10-7 s + 0.2*10-7= 5.97*10-7 s
| x' = 216.3 m - 8.7 = 207.6 m
Es1 = | t' = -4.20*10-8 s + 0.2*10-7= -0.22*10-7 s
| x' = -6.0 m - 8.7 = -14.7 m
Es2 = | t' = 1.00*10-6 s + 0.2*10-7 = 1.02*10-6 s
| x' = 324.6 m - 8.7 = 315.9 m
E2 = | t' = 2.1*10-7 + 0.2*10-7 = 2.3*10-7 s
| x' = 80.2 m - 8.7 = 71.5 m
|
|
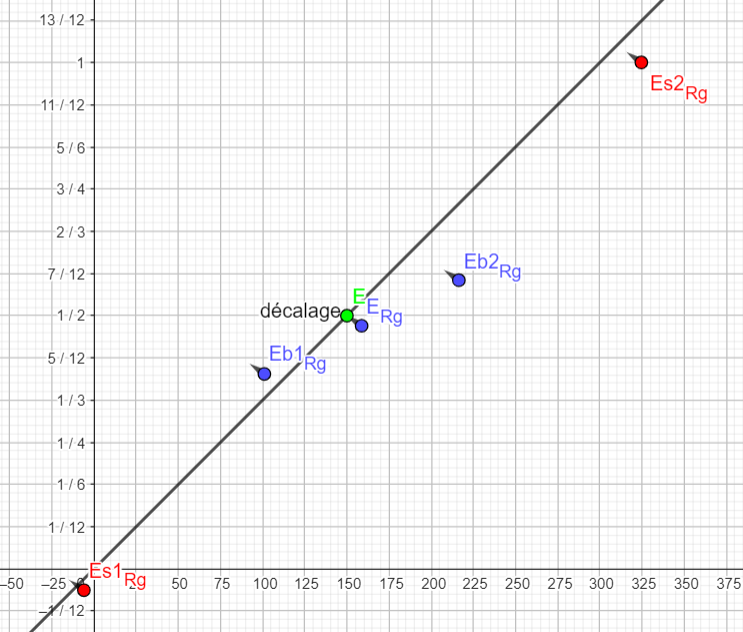
Maintenant que j'ai les coordonnées de Es1 et Es2 dans ce référentiel, je peux les placer.
|
Maintenant que j'ai les coordonnées de Eb1 et Eb2 dans ce référentiel, je peux les placer.
|
Maintenant que j'ai les coordonnées de Es1, Es2, Eb1 et Eb2 dans ce référentiel, je peux les placer.
|
Ajout des lignes de temps et "contraction" de l'espace
Ce qu'il faut remarquer dans la contraction des distances c'est que :
Dans le référentiel propre (celui où l'on se positionne), toutes autres distances dans des référentiels différents au référentiel propre se trouvent contractées. Ce qui crée une illusion de paradoxe. En effet, puisque si Rg voit l'espace se contracter pour Rs, alors comment Rs voit lui aussi l'espace de Rg se contracter, qui dit vrai ? où est la cohérence ? Peut-on sortir de l'un ou l'autre de ses 2 points de vue et prendre un point de vue neutre ?
Eh bien non, sortir de ces 2 référentiels, c'est se placer dans un troisième référentiel qui lui aussi aura son espace-temps propre.
La contraction de l'espace n'est qu'un effet relativiste depuis un référentiel donné. Comme peut l'être la sirène des pompiers qui n'a pas le même son quand le véhicule s'approche ou s'éloigne de l'observateur (effet doppler-fizeau). Le son émit ne se modifie pas, tout comme l'espace de l'autre référentiel.
| ℜg | ℜs | ℜo |
|
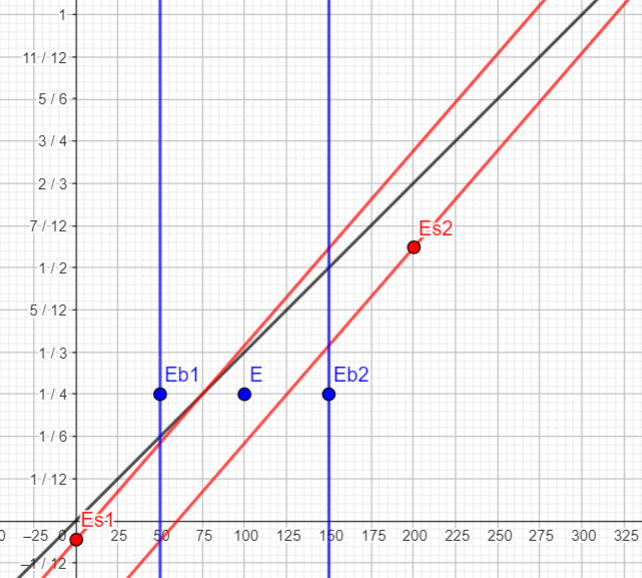
Dans ce référentiel, les bombes ne change pas de position au cours du temps d'où les droites bleues parallèle à l'axe des temps. En revanche, le vaisseau avance à la vitesse 260*106 m.s-1 d'où les droites rouges |
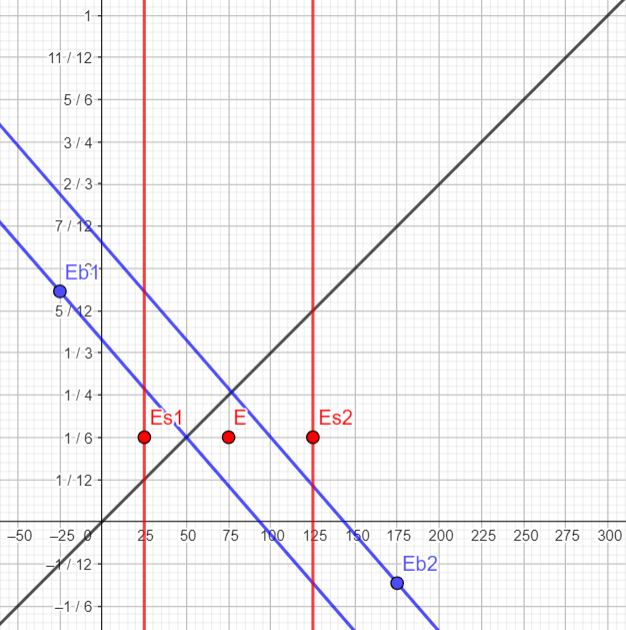
Dans ce référentiel, le vaisseau ne change pas de position dans le temps d'où les droites rouge parallèle à l'axe des temps. En revanche, les bombes avance à la vitesse -260*106 m.s-1 d'où les droites bleues |
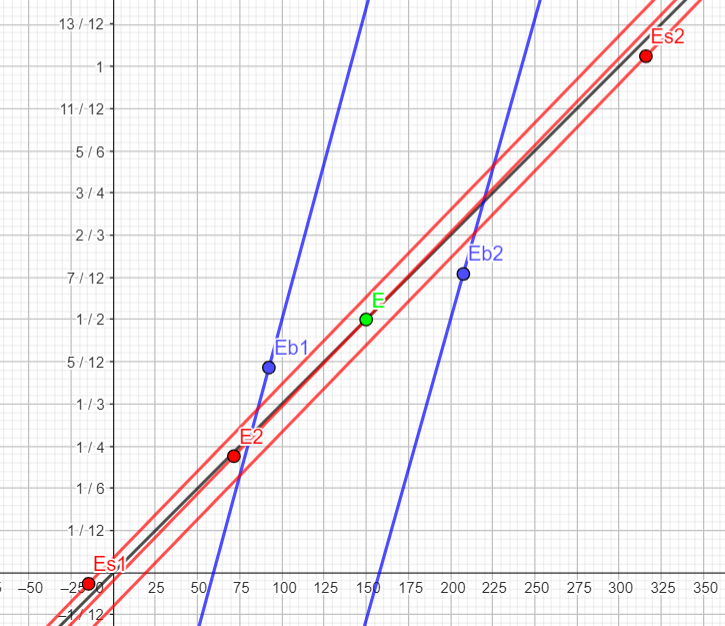
Dans ce référentiel, les bombes s'éloignent à la vitesse 150*106 m.s-1 d'où les droites bleues. Le vaisseau s'éloignent encore plus vite d'où les droites rouges. |
 |
 |
 |
|
Interprétation : Un peu après -1/12μs, L'arrière du vaisseau est à 50m de la bombe lorsque le centre du vaisseau est quant à lui au milieu des 2 bombes bien que dans ce référentiel, le centre du vaisseau n'est pas encore entre les 2 bombes. Aucune bombe n'a encore explosé. Elles exploseront plus tard. Concernant l'avant du vaisseau. Il est à la position de la bombe b1 mais attention, ca ne correspond pas au moment où le centre du vaisseau est au centre des 2 bombes, cela correspond à un moment où le centre du vaisseau n'est pas encore au centre des 2 bombes. Il faut comprendre que la relative contraction des distances à cet instant correspond à des positions de vaisseau à des moments différents. C'est pour cela qu'il n'y pas contraction réelle de l'espace. A 1/6μs, L'arrière du vaisseau est à l'endroit de la bombe, la bombe b1 n'a pas encore explosé. Le centre du vaisseau n'est donc plus au centre des 2 bombes. A 1/4 μs, Les 2 bombes explosent. Le centre du vaisseau est donc bien au milieu des 2 bombes. Pourtant l'arrière du vaisseau à passer la bombe de 25m. L'avant du vaisseau n'a pas encore dépassé la bombe b2. A 1/3 μs, l'avant du vaisseau dépasse la position de la bombe qui a déjà explosé. Un peu avant 1/2μs, l'avant du vaisseau est à 50m de la bombe Conclusion : le vaisseau est indemne. |
Interprétation : Un peu avant -1/12μs, la bombe b2 explose à 50m de s2. Il n'y a donc pas dégât. La bombe b1 est quant à elle au niveau de s2 à ce moment là. Un peu avant 1/12μs, la bombe b2 qui a déjà explosé arrive à s2. La bombe b1 est quant à elle au niveau du centre du vaisseau. A 1/6 μs, le centre des 2 bombes se situe au milieu du vaisseau. le bombe b2 qui a déjà explosé arrive au niveau du milieu avant du vaisseau. La bombe b1 qui n'a pas encore explosé est quant à elle au niveau du milieu arrière du vaisseau. La distance des 2 bombes est contractés mais c'est une distance qui n'est pas celle correspondant au moment où les 2 bombes explosent. Un peu après 1/4μs, la bombe b1 qui n'a pas encore explosé arrive au niveau de l'arrière du vaisseau. La bombe b2 qui a déjà explosé arrive au centre du vaisseau. Un peu avant 1/2μs, la bombe b1 explose à 50m du vaisseau. Il n'y a donc pas dégât. La bombe b2 arrive à l'arrière du vaisseau. Conclusion : le vaisseau est indemne. |
Interprétation : Un peu avant 0 μs, l'arrière du vaisseau est à un peu plus de 50m de la position de la bombe b1 qui n'a pas encore explosé. A 1/4 μs, On oublie l'évenement E2. Je l'ai juste calculé pouvoir représenter la droite rouge du centre pour connaitre le coeff directeur . A 5/12 μs, la bombe b1 explose, l'arrière du vaisseau à passé cette position depuis 25m environ. Le vaisseau est indemne A 1/2 μs, le centre du vaisseau est au centre des 2 bombes. b1 a déjà explosé et b2 n'a pas encore explosé. A 7/12 μs, la bombe b2 explose et l'avant du vaisseau n'a pas encore passé la bombe b2. A 1 μs, l'avant du vaisseau est à 100m de la bombe b2 qui a déjà explosé. Conclusion : le vaisseau est indemne. |
Ce qui est remarquable
Les événements ne se déroulent pas dans le même ordre. La bombe b1 explose avant, en même temps ou après la bombe 2 selon le référentiel. Les positions des vaisseau avant et arrière ont lieu soit en même temps ou avec un décalage.
Pourtant dans tous les cas l'arrière du vaisseau dépassera toujours la position de la bombe avant qu'elle explose. L'avant du vaisseau dépassera toujours la position de la bombe après qu'elle explose.
Calcul des distances entre les événements
Calculons donc (Es1-Eb1) et (Es2-Eb2) dans les 3 référentiels.
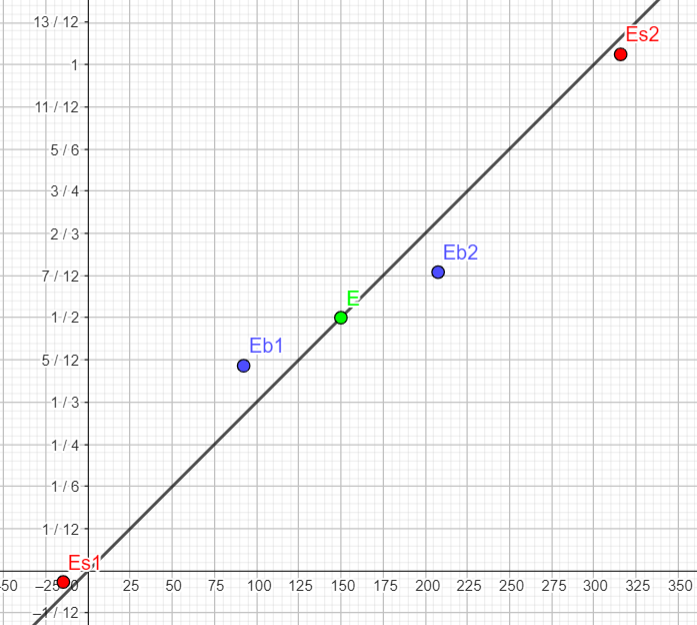
| ℜg | ℜs | ℜo |
|
Eb1 = | t = 1/4μs
| x=50m
Eb2 = | t = 1/4μs
| x=150m
Es1 = | t = -3.70*10-8 s
| x = 0.32 m
Es2 = | t = 5.40*10-7 s
| x = 200.3 m
|
Eb1 = | t = 4.55 * 10-7 s
| x = -25
Eb2 = | t = -1.214 * 10-7 s
| x = 175 m
Es1 = | t = 1/6μs
| x=25m
Es2 = | t = 1/6μs
| x=125m
|
Eb1 = | t = 4.05*10-7 s
| x = 92.3 m
Eb2 = | t = 5.97*10-7 s
| x = 207.6 m
Es1 = | t = -0.22*10-7 s
| x = -14.7 m
Es2 = | t = 1.02*10-7 s
| x = 315.9 m
|
|
(Es1- Eb1)² = - c² ( Es1t - Eb1t )² + (Es1x - Eb1x)² = - 9*1016 * (-3.7*10-8 - 0.25*10-6 )² + (0.32 - 50)² = - 9*1016 * (-2.87*10-7 )² + 2468.10 = - 9*1016 * 8.236*10-14 + 2468.10 = - 7413.21 + 2468.10 = - 4945.11 m² |
(Es1- Eb1)² = - c² ( Es1t - Eb1t )² + (Es1x - Eb1x)² = - 9*1016 * (1/6*10-6 - 4.55*10-7 )² + (25 - -25)² = - 9*1016 * (-2.883*10-7 )² + 2500 = - 9*1016 * 8.313*10-14 + 2500 = - 7482.25 + 2500 = - 4982.25 m² |
(Es1- Eb1)² = - c² ( Es1t - Eb1t )² + (Es1x - Eb1x)² = - 9*1016 * (-0.22*10-7 - 4.05*10-7 )² + (-17.7 - 92.3)² = - 9*1016 * (-4.27*10-7 )² + 12100 = - 9*1016 * 1.823*10-13 + 12100 = - 16409.61 + 12100 = - 4309.61 m² |
|
(Es2- Eb2)² = - c² ( Es2t - Eb2t )² + (Es2x - Eb2x)² = - 9*1016 * (5.4*10-7 - 0.25*10-6 )² + (200.3 - 150)² = - 9*1016 * (2.9*10-7 )² + 2530.09 = - 9*1016 * 8.41*10-14 + 2530.09 = - 7569 + 2530.09 = - 5038.91 m² |
(Es2- Eb2)² = - c² ( Es2t - Eb2t )² + (Es2x - Eb2x)² = - 9*1016 * (1/6*10-6 - - 1.214*10-7 )² + (200.3 - 150)² = - 9*1016 * (2.88*10-7 )² + 2530.09 = - 9*1016 * 8.298*10-14 + 2530.09 = - 7468.41 + 2530.09 = - 4938.32 m² |
(Es2- Eb2)² = - c² ( Es2t - Eb2t )² + (Es2x - Eb2x)² = - 9*1016 * (1.02*10-6 - 5.97*10-7 )² + (315.9 - 207.6)² = - 9*1016 * (-4.23*10-7 )² + 11728.89 = - 9*1016 * 1.78929*10-13 + 11728.89 = - 16103.61 + 11728.89 = - 4375.61 m² |
Il y'a bien une distance non nul entre les éléments du vaisseau et les bombes lorsque les événements se produisent. On peut donc en conclure sans ambiguité que le vaisseau n'explose pas.