L'énoncé
Le paradoxe des jumeaux dit que si je m'éloigne de toi alors je te vois m'éloigner de moi tout comme tu me vois m'éloigner de toi. Et aussi inversement, si je me rapproche de toi alors je me vois me rapprocher de toi tout comme tu me vois me rapprocher de toi. Comme l'effet est symétrique, l'un et l'autre doivent, pour un éloignement et un rapprochement donné, revenir au même âge car rien ne permet de distinguer celui qui s'éloigne de celui qui est immobile. Pourtant la relativité restreinte dit que celui qui s'éloigne et qui se rapproche sera plus jeune que celui qui l'a attendu. Il y'a un donc un paradoxe.
Réponse
Résultat
Prenons Alice et Bob. Bob partira dans une fusée qui ira à la moitié de la vitesse de la lumière. (La vitesse de lumière est nommé en "c", donc la moitié c'est 0.5c).
Alice enverra tous les ans un signal lumineux. Il est convenu que
- au 3ème signal lumineux (soit 3 ans plus tard) : Bob fait demi tour.
- au 9ème signal (soit 9 ans plus tard), Bob repart
- au 12ème signal (soit 12 ans plus tard), Bob revient jusqu'à retrouvé Alice.
Dans la physique classique dite newtonienne, le temps écoulé pour Bob et Alice sera de 24 ans.
Dans la physique relativiste, pour Alice, ce voyage aura duré 24 ans, pour Bob le voyage aura duré 20,8 ans (20 ans et 9 mois 18 jours 7 heures et 12 minutes).
Plus époustouflant, on va constater aussi que bien que Bob reçoit bien le 4ème, 5ème, 6ème et 7ème signal, il va être impossible de se donner une idée du moment où les signaux ont été émis lorsqu'on s'imagine à la place de Bob bien sûr. Et de ce constat, admettre que, dès lors que Bob quitte Alice, ce qui se passe chez Alice n'a plus de signification temporelle pour lui. Elle peut avoir 1 an ou 100 ans, cela n'a plus de réalité. Dans le meilleur des cas, on pourra simplement dire qu'elle est née puisse qu'on reçoit ses signaux lorsqu'on se situe toujours du point de vue de bob..
Calculs
Je vais me concentrer sur l'analyse graphique qui sont le résultat des calculs. Le détail des calculs sont intégralement dans le fichier LibreOffice joint.
Précisions sur la transformation de Lorentz. Le facteur gamma dans cette article aura la valeur de 1.15. On rappellera que gamma c'est : √ ( 1 / (1 - 0.5c/c² ) ).
"c" vaut 1 dans la suite de l'exercice puisqu'on prendra les années en guise d'unité de temps et les années*lumières en guise d'unité de distance.
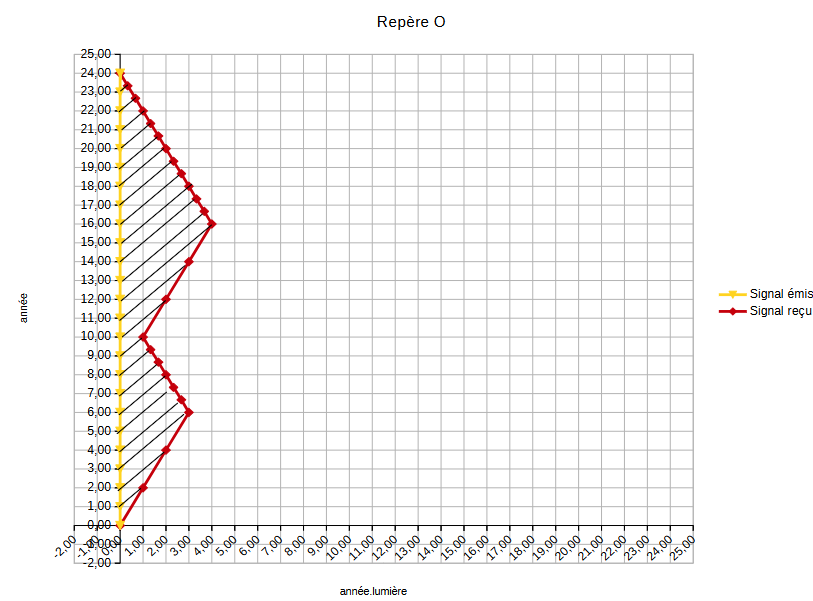
Dans une physique classique, cela se résume par les 2 graphes suivants :
| Le repère O pour originel est celui d'Alice. | |
 |
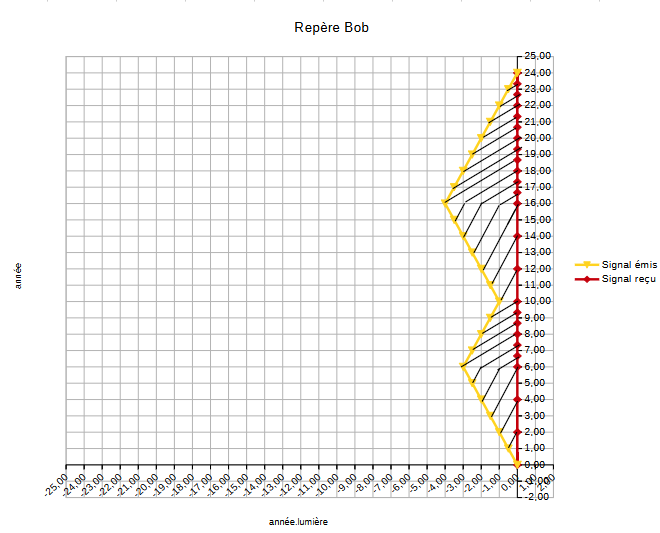 |
Malheureusement, si cette expérience était réalisée dans la réalité, on constaterait au point de rendez-vous un décalage du temps écoulé pour chacune des 2 personnes.
Pour Alice, montre en main, ce voyage aura duré 24 ans.
Pour Bob, montre en main, ce voyage aura duré 20,8 ans (20 ans et 9 mois 18 jours 7 heures et 12 minutes).
La théorie qui explique cela est la relativité restreinte. La gravitation n'intervient donc pas dans ce cas.
Voici les étapes de construction du temps écoulé pour Bob. Je ne détaille pas içi les calculs. Ils sont indiqués dans le fichier LibreOffice.
|
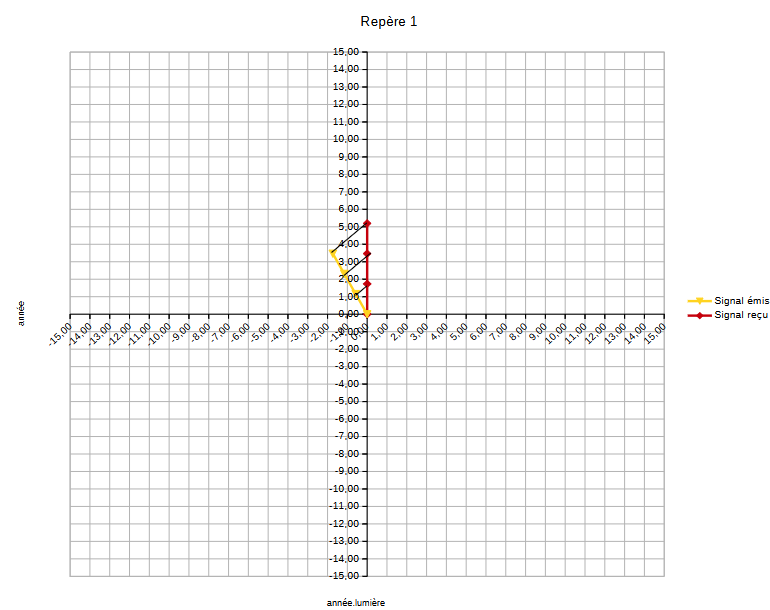
On remarque que Bob reçoit le 3 ème signal non pas dans 6 ans mais dans 5,20 années. Il se rend compte avec les données qu'il a que le signal a dû être envoyé à 3.46 années. De plus, il peut mesurer que l'espace entre 2 signaux reçus est un peu inférieur à 2 ans. Suivant donc son plan de voyage, il change de direction. (cf. repère 2) |
 |
|
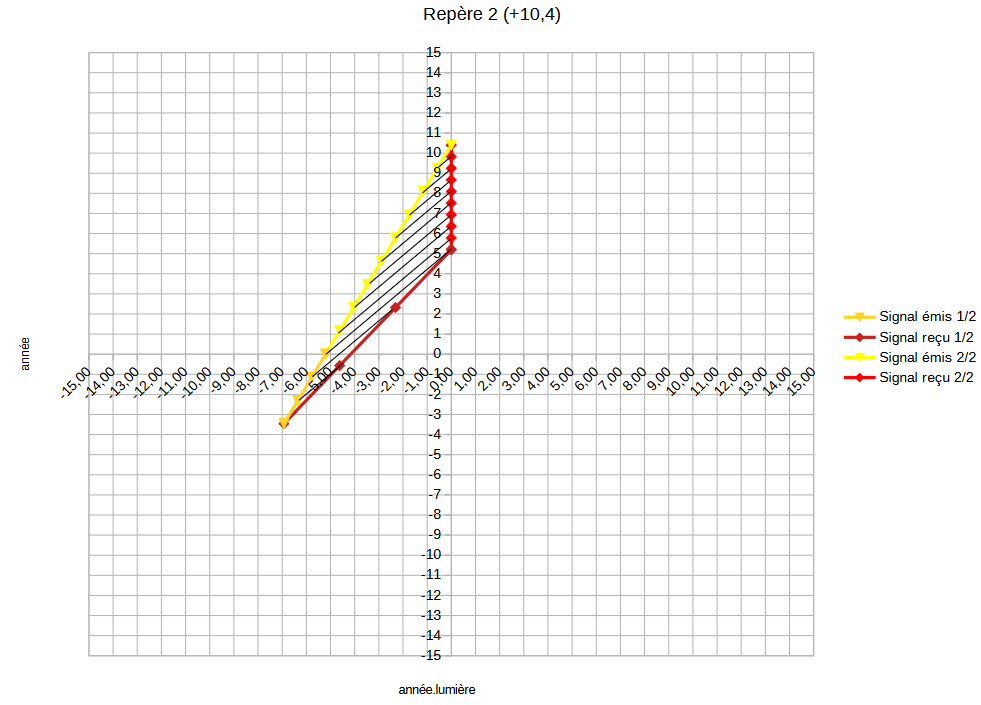
Après avoir changé de direction, voici à quoi ressemble de son point de vue le chemin du retour et la fréquence à laquelle il reçoit les signaux d'Alice. Tant dans le repère précédent, les messages mettaient du temps à arriver tant dans celui ci ils arrivent tous les 0,57 ans. Le modèle classique prévoyait plutôt tous les 0,66 ans. Contrairement à ce schéma où les 2 protagonistes se rejoignent, ils étaient convenu qu'au bout du 9ème signal reçu, Bob change de nouveau de direction en s'éloignant d'Alice. (cf. repère 3) |
 |
| Au bout du 12ème signal, Bob refait demi-tour. (cf. repère 4) | 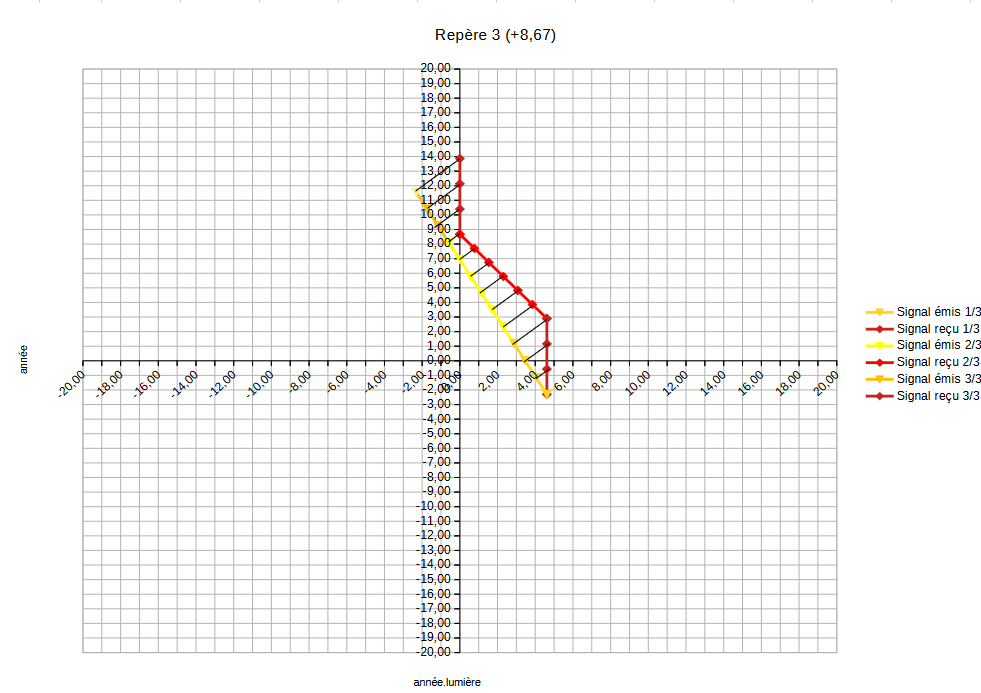 |
| Et voici le dernier repère représentant l'intégralité du voyage. | 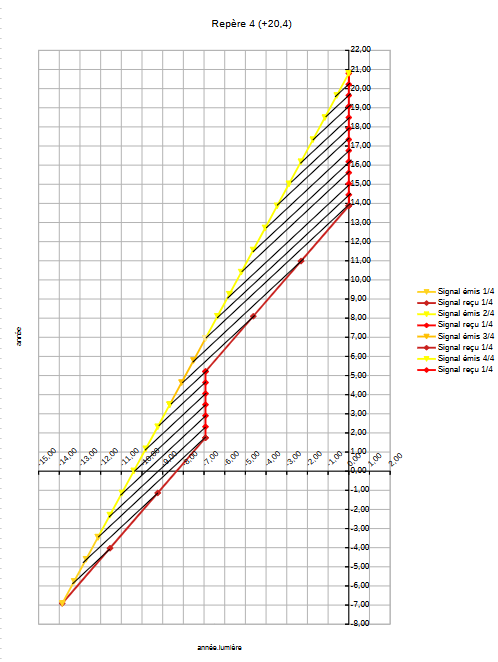 |
De ce résultat, on a d'une part, les 24 signaux envoyés tous les ans d'Alice et tous les temps où ces signaux sont reçus (on prendra soin de prendre le bon repère pour connaitre la date de réception du signal).
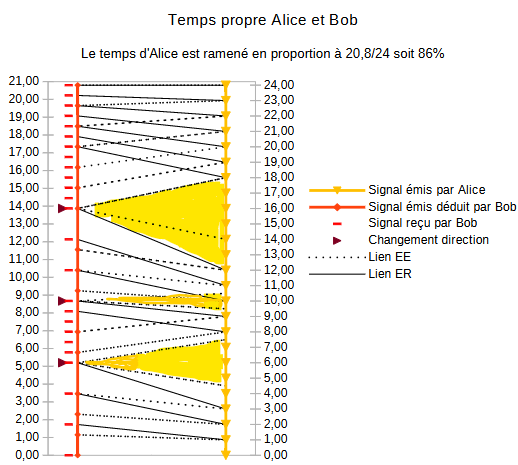
On va donc pouvoir, d'un côté mettre sur une ligne droite, les années de Bob écoulés et les années d'Alice écoulés selon le point de vue de Bob et faire correspondre certains événements. En effet, je ne vais tracer que les événements qui se situent dans la même direction (donc sans changement de direction). Autrement dit je n'indique pas ci-dessous un signal émis par Alice et reçu par Bob qui survient après un changement de direction.
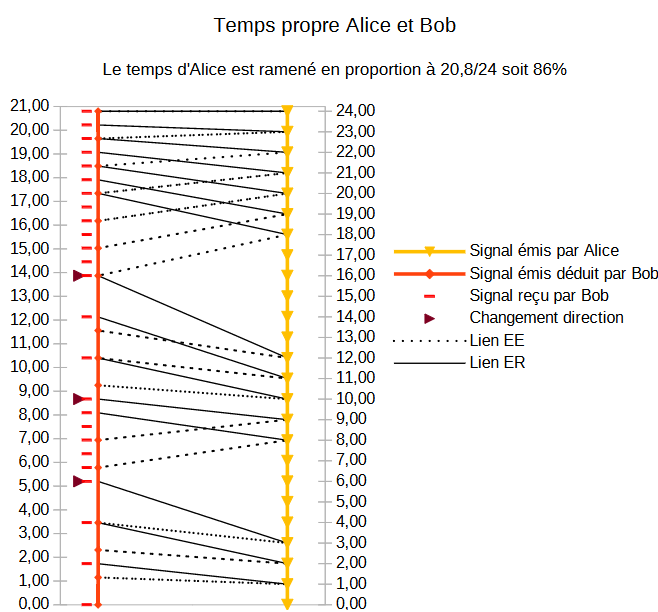
Il y'a beaucoup d'informations sur le schéma ci-dessus et tout n'y est pas représenté. Pour autant :
- Les lignes continues lient d'une part l'événement signal Emis dans le temps d'Alice avec l'événement signal Reçu de Bob (Lien ER)
- Les lignes discontinues lient d'une part l'événement signal Emis dans le temps d'Alice avec l'événement signal Emis déduit de Bob (Lien EE)
- Les 3 flèches horizontales indiquent le moment où Bob change de direction.
On remarque qu'avant chaque changement de direction, il y' a une véritable "inversion" entre l'année ou Alice émet le signal et l'année où Bob déduit l'année où Alice à émit le signal. On va donc s'intéresser au derniers instants avant et après un changement de direction. Autrement dit, si Bob pense qu'Alice a émit son signal de 1 an à 1,15 à 2,31 pour son 2ème signal à 3,46 années pour son 3ème signal. A quelle année correspond chez Alice, l'année 5,20 de Bob ? Pareillement l'année 5,8 de Bob correspondrait à l'émission du 8ème signal chez Alice. A quelle année correspond chez Alice, l'année 5,20 de Bob ?
Ci-dessous, en jaune, ce sont les dates que je cherche à connaitre.
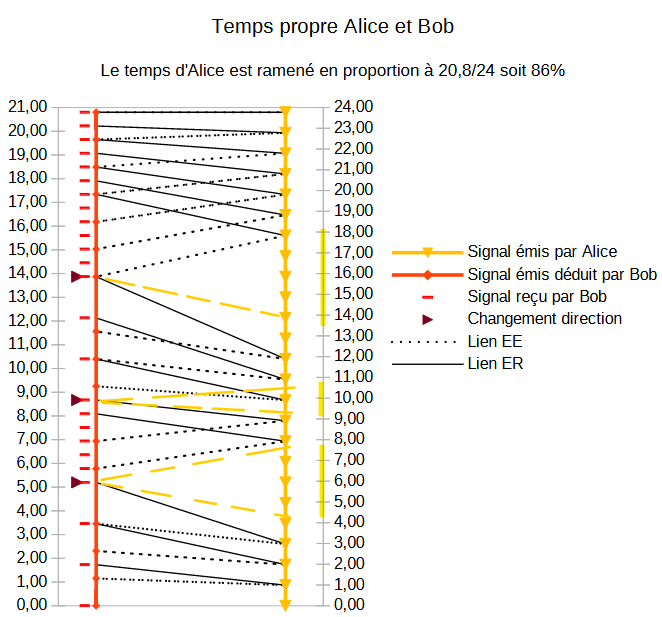
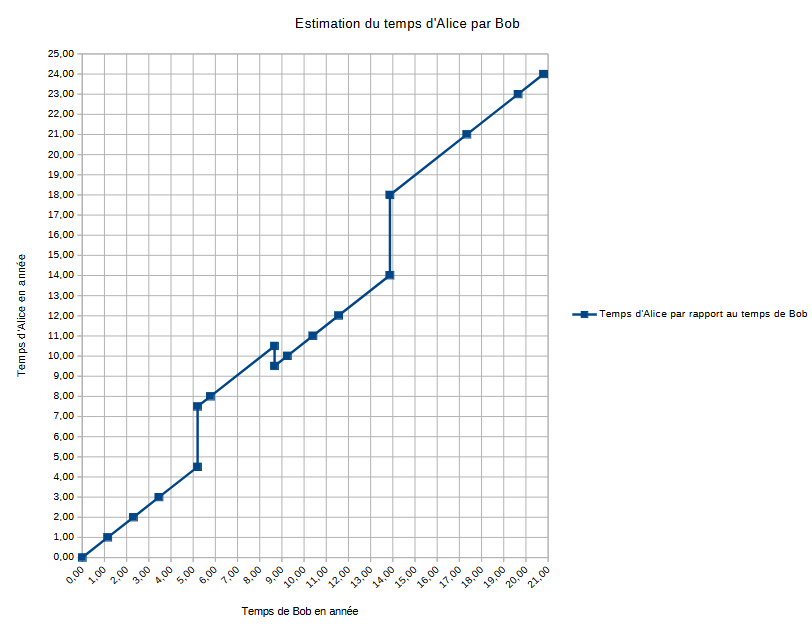
A la date 5,20 en venant du bas, la date d'Alice correspondante est : 4.5 années
A la date 5,20 en venant du haut, la date d'Alice correspondante est : 7.5 années
A la date 8,67 en venant du bas, la date d'Alice correspondante est : 10,5 années
A la date 8,67 en venant du haut, la date d'Alice correspondante est : 9.5 années
A la date 13.87 en venant du bas, la date d'Alice correspondante est : 14 années
A la date 13.87 en venant du haut, la date d'Alice correspondante est : 18 années
Pour 5,20 et 13,87, il ne s'agit pas de vieillissement en un bond d'Alice ni encore moins d'un rajeunissement d'un coup d'Alice à la date de 8,67, ce qui n'a encore moins de sens. D'ailleurs, à chaque date de changement de direction, il existe bien 2 dates pour Alice. Une date pour une direction de Bob et une autre dans pour une autre direction de Bob. Il y'a une simultanéité de dates. Il est d'ailleurs de 2 dates et non de toutes les dates entre celles-ci ce qui est d'autant plus absurde c'est que un bond de 4.5 années à 7.5 années n'empêche pas Bob de recevoir les signaux des années, 5,6 et 7 années d'Alice.
Par extension de ces résultats, dès lors que Bob quitte Alice par un déplacement relatif à Alice, le temps d'Alice devient complètement étranger à celui de Bob, tout comme c'est le cas pour Alice où le temps de Bob lui devient complètement étranger, c'est à dire sans réalité physique.

